微分几何笔记(一)——曲线
Section 1
参数曲线
定义:一个光滑映射(无穷阶可导)![\[ \phi : I \to R^3\] \[ \phi : I \to R^3\]](/user_files/Dantepy/epics/09258b7cbe179a7de12ee69c07b0f84447adc372.png) 称为参数化曲线。
称为参数化曲线。
注:两条不同的参数化曲线可以有相同的轨迹,这是因为你对I作一个同胚,就得到一个不同的映射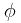 ,但是它们有相同的轨迹。
,但是它们有相同的轨迹。
参数化正则曲线
定义:若对参数曲线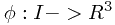 有
有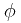 '
'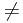 0,则称
0,则称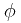 为正则参数曲线。
为正则参数曲线。
注:使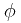 '=0 的点我们称之为奇异点。
'=0 的点我们称之为奇异点。
弧长
因为参数化曲线的形式太任意了,所以我们引出弧长的定义:
定义:设 是正则参数曲线,
是正则参数曲线, ,当参数从
,当参数从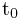 到
到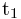 时,曲线的弧长为
时,曲线的弧长为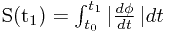 .
.
注意:弧长是不会因为参数化的形式而变化的,因为根据定义,当参数化形式变化的时候,只需要对S中的积分作一个变量代换即可。
用弧长来定义曲线
由弧长的定义可得![\[ \frac{dS}{dt} = |\frac{d \phi}{dt}| > 0\] \[ \frac{dS}{dt} = |\frac{d \phi}{dt}| > 0\]](/user_files/Dantepy/epics/a47c608d35c4583e35473452f60104ebb3c97432.png) ,所以,S和t存在可逆变换,于是,我们可以用弧长来做曲线的参数:
,所以,S和t存在可逆变换,于是,我们可以用弧长来做曲线的参数:![\[\tilde{\phi} (S) = \phi (t(S)) \] \[\tilde{\phi} (S) = \phi (t(S)) \]](/user_files/Dantepy/epics/32ab3ec921c47db02b72edf6b27f4db364de7dd1.png)
注意:在给定定向之后,弧长参数在差一个常数的意义下唯一
我们可得:![\[ |\frac{d \phi}{d S}| \equiv 1\] \[ |\frac{d \phi}{d S}| \equiv 1\]](/user_files/Dantepy/epics/3ff403b6ca3679a2a2b22ac77981cbd83beb0a9b.png) 反之若有参数化曲线
反之若有参数化曲线 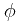 使得
使得 ![\[ |\frac{d \phi}{d t}| \equiv 1\] \[ |\frac{d \phi}{d t}| \equiv 1\]](/user_files/Dantepy/epics/a78568a03583ffd3de8423007d62f2776e3209bb.png) ,则t为弧长参数。证明是很容易的啦。
,则t为弧长参数。证明是很容易的啦。
切向量、主法向量和从法向量
首先让我们考虑向量场的内积。
假设![\[ \phi(S)\] \[ \phi(S)\]](/user_files/Dantepy/epics/9c6206b212aa047d689ae170b0709e0e7618f667.png) 是弧长参数化的曲线,则对
是弧长参数化的曲线,则对![\[ \phi\] \[ \phi\]](/user_files/Dantepy/epics/1a90d6594e2ee16efda2db0ad1e808326697462e.png) 有
有![\[ |\dot{\phi}(S) |\equiv 1\] \[ |\dot{\phi}(S) |\equiv 1\]](/user_files/Dantepy/epics/a334d1008ac51a01ccb295d64b7f2e0b8f0ac0d9.png) (
(![\[ \dot{\phi}(S) \] \[ \dot{\phi}(S) \]](/user_files/Dantepy/epics/5d08f0c7a0ca0b12cb101140a23cd5a695ecbacf.png) 表示
表示![\[ {\phi}(S) \] \[ {\phi}(S) \]](/user_files/Dantepy/epics/a2b6151b6f64bcc69d0c1e8d1e8a6e8a3c4277ac.png) 的导数).
的导数).
由此可以推出:![\[ \dot{\phi}(S) \cdot \dot{\phi}(S) \equiv 1\] \[ \dot{\phi}(S) \cdot \dot{\phi}(S) \equiv 1\]](/user_files/Dantepy/epics/18eee6e20e97125be14561d99bdf03894e6b8487.png) ,对此式求导,可得
,对此式求导,可得![\[ \dot{\phi}(S) \cdot \ddot{\phi}(S) \equiv 0\] \[ \dot{\phi}(S) \cdot \ddot{\phi}(S) \equiv 0\]](/user_files/Dantepy/epics/c00c15782c190fa59311fe1a9c2986f73a3a6bed.png) (*)
(*)
定义:称![\[ k(s) = |\ddot{\phi}(s)|\] \[ k(s) = |\ddot{\phi}(s)|\]](/user_files/Dantepy/epics/8569f1920991e3fe0af2815f429dda288b61fdce.png) 中
中![\[ k(s) \] \[ k(s) \]](/user_files/Dantepy/epics/818155332b09dedcb05543ae4a7cbc7e3e0c5834.png) 为
为![\[ \phi\] \[ \phi\]](/user_files/Dantepy/epics/1a90d6594e2ee16efda2db0ad1e808326697462e.png) 在s处的曲率。
在s处的曲率。
定义:记![\[ \vec{t}(s) = \dot{\phi}(s) \] \[ \vec{t}(s) = \dot{\phi}(s) \]](/user_files/Dantepy/epics/7421334df39930c0adfd70c726db1f3fd3d50f89.png) ,称
,称![\[ \vec{t}(s) \] \[ \vec{t}(s) \]](/user_files/Dantepy/epics/7ad8e36677366666d84f48d586b48533301f283b.png) 为
为![\[ \phi(s) \] \[ \phi(s) \]](/user_files/Dantepy/epics/9e76480f8e78dc57c3db6fc4546d6c61f3318122.png) 在s处的切向量
在s处的切向量
定义:记![\[ \vec{n}(s) = \frac{\ddot{\phi}(s)}{k(s)} \] \[ \vec{n}(s) = \frac{\ddot{\phi}(s)}{k(s)} \]](/user_files/Dantepy/epics/dc5149a6d945c30182e62351fd2d82a489999157.png) ,称
,称![\[ \vec{n}(s) \] \[ \vec{n}(s) \]](/user_files/Dantepy/epics/c6194bdd9e9c74c76a5ac987b27b0e8f1078e40c.png) 为
为![\[ \phi(s) \] \[ \phi(s) \]](/user_files/Dantepy/epics/9e76480f8e78dc57c3db6fc4546d6c61f3318122.png) 在s处的主法向量。 由(*)可知,
在s处的主法向量。 由(*)可知,![\[ \vec{n}(s) \] \[ \vec{n}(s) \]](/user_files/Dantepy/epics/c6194bdd9e9c74c76a5ac987b27b0e8f1078e40c.png) 与
与![\[ \vec{t}(s) \] \[ \vec{t}(s) \]](/user_files/Dantepy/epics/7ad8e36677366666d84f48d586b48533301f283b.png) 垂直(正交),而且这两个向量的模都是1.
垂直(正交),而且这两个向量的模都是1.
定义:记![\[\vec{b}(s)=\vec{t}(s) \times \vec{n}(s)\] \[\vec{b}(s)=\vec{t}(s) \times \vec{n}(s)\]](/user_files/Dantepy/epics/dac141df18b7cfec48c45b174486ac72dfc3bd74.png) ,称
,称![\[\vec{b}(s)\] \[\vec{b}(s)\]](/user_files/Dantepy/epics/8b9edc5dbee79c7ee554b09b6cc6d8e104fd0ad0.png) 为
为![\[ \phi(s) \] \[ \phi(s) \]](/user_files/Dantepy/epics/9e76480f8e78dc57c3db6fc4546d6c61f3318122.png) 在s处的从法向量。 这个向量与切向量和主法向量都垂直,而且模是1,所以
在s处的从法向量。 这个向量与切向量和主法向量都垂直,而且模是1,所以![\[\{ \vec{t}\ \vec{n}\ \vec{b} \}\] \[\{ \vec{t}\ \vec{n}\ \vec{b} \}\]](/user_files/Dantepy/epics/64f161d0c9876bf16ca260f0057c30441218e1cb.png) 构成
构成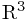 正交基底。
正交基底。
当然,这个基底还不足以完全描述曲线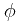 的行为,我们需要这三个向量和对这三个向量求导而得到的微分方程。为此我们对这三个向量求导。
的行为,我们需要这三个向量和对这三个向量求导而得到的微分方程。为此我们对这三个向量求导。
由前面已经可以知道![\[ \frac{d \vec{t}}{ds} = k(s) \vec{n}(s) \] \[ \frac{d \vec{t}}{ds} = k(s) \vec{n}(s) \]](/user_files/Dantepy/epics/555e77446003e9f8cb0cf751703e60d657fb9bee.png) ,
,
我们先考虑![\[ \frac{d\vec{b}(s)}{ds} \] \[ \frac{d\vec{b}(s)}{ds} \]](/user_files/Dantepy/epics/52c606261c5af51b634902c6cb63bbe5a8289e3d.png)
挠率
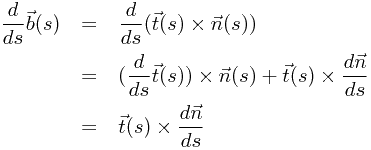
由这条式子,我们可以看到![\[ \frac{d\vec{b}(s)}{ds} \] \[ \frac{d\vec{b}(s)}{ds} \]](/user_files/Dantepy/epics/52c606261c5af51b634902c6cb63bbe5a8289e3d.png) 与
与![\[ \vec{t}(s) \] \[ \vec{t}(s) \]](/user_files/Dantepy/epics/7ad8e36677366666d84f48d586b48533301f283b.png) 是垂直的(因为
是垂直的(因为![\[ \frac{d\vec{b}(s)}{ds} \] \[ \frac{d\vec{b}(s)}{ds} \]](/user_files/Dantepy/epics/52c606261c5af51b634902c6cb63bbe5a8289e3d.png) 是
是![\[ \vec{t}(s) \] \[ \vec{t}(s) \]](/user_files/Dantepy/epics/7ad8e36677366666d84f48d586b48533301f283b.png) 与
与![\[\frac{d\vec{n}}{ds} \] \[\frac{d\vec{n}}{ds} \]](/user_files/Dantepy/epics/1078c9fd0a61b015f015f12d0f0b3d35d1d108b7.png) 叉乘的积),同时
叉乘的积),同时![\[ \frac{d\vec{b}(s)}{ds} \] \[ \frac{d\vec{b}(s)}{ds} \]](/user_files/Dantepy/epics/52c606261c5af51b634902c6cb63bbe5a8289e3d.png) 本身与
本身与![\[\vec{b} \] \[\vec{b} \]](/user_files/Dantepy/epics/b37df84c6b1c1b09126202e37fd748fde08584a8.png) 垂直,所以
垂直,所以![\[ \frac{d\vec{b}(s)}{ds} \] \[ \frac{d\vec{b}(s)}{ds} \]](/user_files/Dantepy/epics/52c606261c5af51b634902c6cb63bbe5a8289e3d.png) 与
与![\[\vec{n} \] \[\vec{n} \]](/user_files/Dantepy/epics/4ce22e96fd3629d98a1f2caf076a5b48917ace9d.png) 平行。从而,我们可以定义:
平行。从而,我们可以定义:![\[\frac{d\vec{b}}{ds} = \tau (s) \vec{n}(s) \] \[\frac{d\vec{b}}{ds} = \tau (s) \vec{n}(s) \]](/user_files/Dantepy/epics/69f42f73cd53b6e72cd8d6d9961fd1d4dffbd890.png) .由此得出:
.由此得出:
定义:我们称![\[ \tau(s) \] \[ \tau(s) \]](/user_files/Dantepy/epics/898b72441d73c06e5b1435e311ca1531f049b85c.png) 为曲线的挠率
为曲线的挠率
在此基础上,我们继续讨论![\[ \frac{d\vec{n}}{ds}\] \[ \frac{d\vec{n}}{ds}\]](/user_files/Dantepy/epics/9edd30eb04237c51ecf36b7cbb629da0a8e02cd9.png)
因为
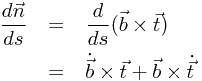
所以,我们可以最后化简得:
![\[ \dot{\vec{n}} = -\tau \vec{b}-k\vec{t}\] \[ \dot{\vec{n}} = -\tau \vec{b}-k\vec{t}\]](/user_files/Dantepy/epics/362e0bebc334e75f0a86065418f6b09a6a5395cf.png)
综上,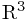 中的曲线可以如下的微分方程组来描述:
中的曲线可以如下的微分方程组来描述:
![\[ \frac{d}{ds} (\vec{t},\vec{n},\vec{b}) &=& A(\vec{t},\vec{n},\vec{b})\] \[ \frac{d}{ds} (\vec{t},\vec{n},\vec{b}) &=& A(\vec{t},\vec{n},\vec{b})\]](/user_files/Dantepy/epics/692ea3ad5b4eff0e7e3ae3c57da4593d2a028efd.png) 其中
其中 ![\[ A &=& \left( \begin{array}{ccc}0&k&0\\-k&0&-\tau\\ 0&\tau&0 \end{array} \right)\] \[ A &=& \left( \begin{array}{ccc}0&k&0\\-k&0&-\tau\\ 0&\tau&0 \end{array} \right)\]](/user_files/Dantepy/epics/d87d0870bba5a2d7a3a42b31de823bd602689c01.png) .
.
 评论 (0)
评论 (0)