数计之宅

1、定义

     压缩映射：设R为完备度量空间，A为R到其本身的映射，如果存在数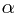< 1使得对于R中任意两点x,y满足不等式：

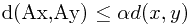
      则称A为压缩映射或者压缩。

     不动点：如果Ax=x，则x为映射A的不动点。

2、定理

     在完备度量空间定义的任一压缩映射有且仅有一个不动点。

3、关于定理的证明及其思考

      在柯尔莫戈洛夫的《函数论与泛函分析初步》中，这个定理的证明思路如下：1）存在性，在一个完备度量空间中，任意一点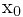，将压缩映射A作用在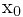上，得到一个点列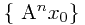，这个点列是基本列，而在完备度量空间中，它必然收敛，然后证明其极限点即为A的不动点即可；2）唯一性，利用压缩映射定义中的不等式。

      问题：为什么是？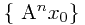

      一个直观的解答：我们可以先考虑一个有界的度量空间R，在压缩映射A的作用下，R的“体积”是不断变小的，经过无穷次压缩之后，它可以被“压缩"成一个点（这一点可以由其完备性保证）。

      以上想法的缺陷：1、无界的完备度量空间的情况如何考虑？2、当我写下这篇文章的时候我还没有想到。

      这种想法的应用：

       在柯尔莫戈洛夫的书中有一道习题：举例说明对一切x不等于y满足d(Ax,Ay)小于d(x,y)的映射A，可能连一个不动点都没有。我们找一个映射，使之不能把度量空间的体积变小即可。